Splay Tree 1. 개념과 사용
BST(Binary Search Tree)의 한 종류인 Splay tree는, Splay라는 rotation 기반의 간단한 연산을 통해 쿼리를 할 때마다 Self Balancing을 수행한다. Splay tree는 다른 Balanced Binary Search Tree보다 구현이 (알고리즘 대회에서 구현 할 수 있을 만큼) 간단하고, 다양한 종류의 쿼리를 $amortized \space O(\log n)$시간에 수행 할 수 있다.
본 글은 읽는 이가 segment tree, lazy propagation, binary search tree에 대한 기본적인 지식이 있다고 가정한다.
Splay
Splay는 Splay tree의 기본이 되는 연산으로, 쿼리에 의해 접근한 노드를 트리 구조에 따라 특정 방식으로 rotate해서 루트까지 끌어올리는 연산이다. 트리의 구조에 따라 rotate하는 세 가지 방법을 zig, zig-zig, zig-zag라고 한다. 쿼리에 의해 접근한 노드가 x라고 하자.
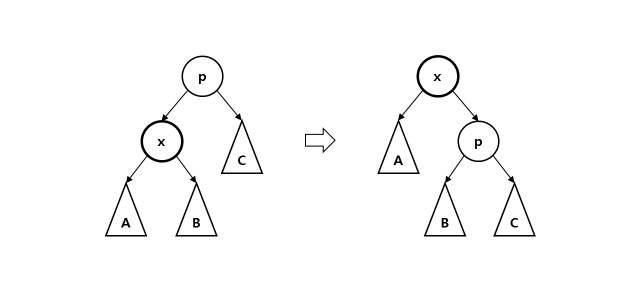
zig step: x가 parent가 있고 grandparent는 없을 때 rotate(x)한다.
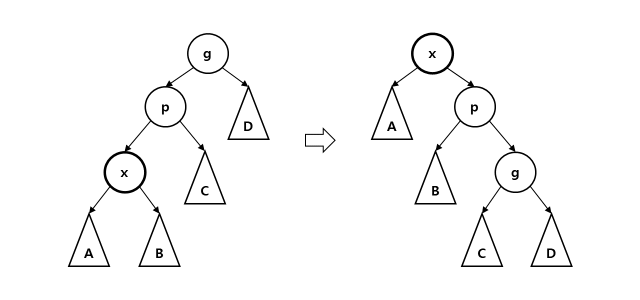
zig-zig step: x와 parent가 둘 다 left child거나 둘 다 right child면 rotate(parent)한 후 rotate(x)한다.
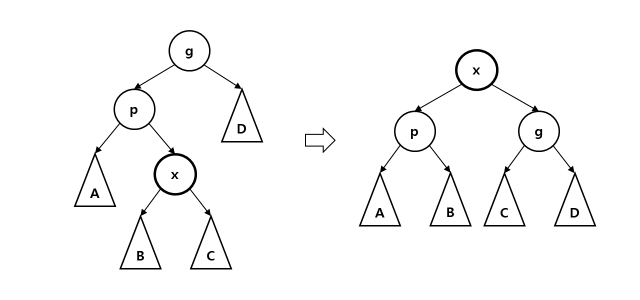
zig-zag step: x가 left child고 parent가 right child거나 그 반대의 경우 rotate(x)를 두 번 한다.
트리의 구조에 따라 zig, zig-zig, zig-zag 중 하나를 수행한 후, x가 루트가 아니라면 다시 반복한다. 따라서 splay가 끝나면 x는 트리의 새 루트가 된다. 당연하지만 일반적인 BST에서처럼 rotate후에도 노드들의 정렬(inorder 순서)이 유지된다.
앞으로 설명할 splay tree의 모든 연산은 splay를 사용한다. Splay를 통해 트리가 self balancing하기 때문에, 초기 트리가 degenerate하더라도 충분히 많은 쿼리를 수행하면 모든 쿼리가 $amortized \space O(\log n)$시간에 동작한다.
기본 연산 (삽입, 검색, 삭제)
접근한 원소를 splay한다는 차이점을 제외하면 일반적인 BST와 유사하다.
삽입: 일반적인 BST처럼 루트에서 시작해 내려가다 알맞은 위치에 새 노드를 삽입한다. 그리고 새로 삽입한 노드를 splay한다.
검색: 마찬가지로 일반적인 BST에서 하듯이 노드를 찾은 후 그 노드를 splay한다.
삭제: 삭제할 노드를 검색한다. 삭제할 노드가 새 루트이므로 루트를 삭제하면 루트의 양쪽 subtree가 분리되므로 이를 연결해야 한다. Left subtree의 가장 큰 원소(rightmost element)를 x라고 하자. Right subtree를 x의 right child로 만들고 x를 splay하면 두 subtree를 연결할 수 있다.
응용 연산
1. k번째 원소 찾기
k번째 원소(노드)를 검색하기 위해선 각 노드가 자신의 subtree의 size 정보를 관리하도록 해야 한다. Splay 연산에서 rotation을 할 때 child가 바뀌므로 이런 노드에 대해 rotate후 subtree size를 다시 계산해준다. 삽입이나 삭제 연산같이 어떤 노드에 새로운 child를 추가하는 경우를 생각해보자. 해당하는 child가 splay되어 루트로 올라가므로 splay의 rotation 연산에서 업데이트를 처리하면 루트까지 이어지는 path에 있는 모든 노드의 subtree size가 알맞게 업데이트될 것이다.
각 노드가 subtree size를 알고 있다면, k번째 원소를 찾는 것을 검색 연산과 비슷하게 구현할 수 있다. 편의성을 위해 k를 0-base로 하자. 루트에서 시작해 현재 노드의 left child의 subtree size를 본다. 이 값을 x라고 할 때,
- x가 k와 같으면 현재 노드보다 작은 원소가 k개 있다는 뜻이므로 현재 노드가 내가 찾는 원소이다.
- x가 k보다 크다면 k번째 원소는 left subtree에 속해 있으므로 left child로 이동한 후 반복한다.
- x가 k보다 작다면 k번째 원소는 right subtree에 속한 원소 중 k - x - 1번째 원소이므로 k -= x + 1 한 후 right subtree로 이동한 후 반복한다.
k번째 원소를 찾으면 그 원소를 splay한다.
2. 수열의 구간에서 max(혹은 min, sum 등)값 찾기
Splay tree로 수열을 표현해 수열에 range query를 빠르게 처리 할 수 있다. BST의 정렬을 노드의 item(수열의 원솟값)으로 하는 게 아니라 수열의 index로 한다는 점이 중요하다. 위에서 설명한 k번째 원소를 찾는 기능과 더불어, 각 노드가 subtree의 max 값도 관리하도록 해야 한다. 이제 subtree size를 업데이트할 때 subtree의 max 값도 업데이트한다.
$[l, \space r]$ 구간에서 max 값을 구하려면, 먼저 $l - 1$번째 원소를 찾는 쿼리를 한다. 이제 $l - 1$번째 원소가 splay되었으므로 새 루트이다. 루트의 right subtree에는 $[l, \space n - 1]$구간의 원소들이 모여있다. 잠시 루트에서 right child와의 연결을 끊고 right subtree를 독립된 트리로 취급하자. 이 트리에서 $r - l + 1$번째 원소를 찾는 쿼리를 하면 전체 수열에서 $r + 1$번째 원소가 splay된다. 이 $r + 1$번째 원소는 right subtree의 루트, 즉 새로운 right child가 된다(연결을 끊은 것은 이 쿼리 이후 다시 연결한다). 이 right child의 left subtree는 이제 $[l, \space r]$ 구간의 원소들이 모여있다. 따라서 루트의 right child의 left child의 max값이 $[l, \space r]$의 max 값이 된다.

위 방식은 $l = 0$ 이거나 $r = n - 1$ 인 경우를 따로 처리해 주어야 한다. 이것이 싫다면 -1번 index와 n번 index를 가지는 가상의 dummy 노드를 넣으면 된다.
3. 수열에서 point update, range update
하나의 원솟값만 바꾸면 되는 point update의 경우 그 원소를 찾아 splay해 루트로 만든 후 원솟값을 바꿔주면 된다.
연속된 구간의 값을 바꾸는 range update를 $amortized \space O(\log n)$시간에 수행해야 할 경우 lazy propagation을 사용해야 한다. 이를 위해 노드가 lazy 값을 관리한다. Range update를 하기 위해선 먼저 위에서 설명한 방법으로 $[l, \space r]$ 구간의 노드들을 한 subtree에 모은 후 subtree의 루트의 lazy 값을 업데이트해 주면 된다.
어떤 노드의 lazy가 default 값이 아니라는 것은 그 노드의 현재 subtree에 이 lazy 값이 언젠가는 업데이트되어야 한다는 뜻이다. 따라서 subtree가 바뀌기 직전, 혹은 자식의 정보를 당장 사용해야 할 때 자식에게 lazy 값을 전파해주면 된다. 구현하는 range update의 종류에 따라 루트에서 시작해 자식 노드로 내려갈 때 lazy 값을 전파하는 것으로 충분할 수도 있고, 트리 중간의 어떤 노드가 splay를 통해 루트로 올라갈 때 lazy 값을 전파하는 것으로 충분할 수도 있다. 혹은 두 경우 모두 lazy 값을 전파해야 트리가 올바르게 동작할 수도 있다.
4. 수열의 구간 뒤집기, 수열의 구간 shifting
Lazy propagation을 사용하면 수열의 구간을 뒤집는 연산도 $amortized \space O(\log n)$시간에 가능하다. 먼저 각 노드가 lazy 값의 한 종류로 boolean 타입의 reverse 값을 관리해야 한다.
수열의 $[l, \space r]$ 구간을 $[r, \space l]$로 뒤집는 것을 다음과 같이 생각할 수 있다. 구간 사이에 있는 임의의 index를 골라 $x$라고 하자. 그러면 구간을 세 구간 $[l, \space x - 1]$, $[x]$, $[x + 1, \space r]$로 쪼갤 수 있다. $[x]$를 기준으로 양옆 두 구간을 맞바꾸면 구간은 $[x + 1, \space r]$, $[x]$, $[l, \space x - 1]$이 된다. 재귀적으로 $[x + 1, \space r]$, $[l, \space x - 1]$를 뒤집으면, 구간이 $[r, \space x + 1]$, $[x]$, $[x - 1, \space l]$이 된다. 따라서 수열의 $[l, \space r]$ 구간을 $[r, \space l]$로 뒤집었다.
따라서 구간을 뒤집는 연산은 $[l, \space r]$ 구간의 노드들을 한 subtree에 모은 후 subtree의 루트의 reverse 값을 업데이트하는 것으로 구현할 수 있다. 이후 lazy propagation을 할 때 reverse가 참일 경우 left child와 right child를 맞바꾸고 자식들의 reverse 값도 업데이트해 주면 된다. 여기서 reverse 값을 업데이트한다는 것은 이전 reverse 값을 반전시킨다는 뜻이다.
Lazy propagation을 하는 타이밍에 유의할 점이 있다. 검색이나 k번째 원소를 찾는 쿼리 등 left child가 가진 값에 따라 행동이 달라지는 쿼리를 할 때, reverse 값을 미리 전파해 left child와 right child를 맞바꿔야 올바르게 작동한다.
구간 뒤집기를 응용하면 수열의 구간 shifting도 구현할 수 있다. 구간 $[a, \space \dots, \space b, \space c, \space \dots, \space d]$를 $[c, \space \dots, \space d, \space a, \space \dots, \space b]$로 shifting하는 것은 전체 구간을 뒤집어 $[d, \space \dots, \space c, \space b, \space \dots, \space a]$로 만든 후 $[d, \space \dots, \space c]$와 $[b, \space \dots, \space a]$를 각각 다시 뒤집는 것과 같기 때문이다.
Splay 구현 코드
Splay tree의 구현은 개념적으로는 어렵지 않지만, 부모 자식 노드 간 연결을 잇거나 끊는 부분과 lazy 값을 전파하는 부분에서 실수하지 않도록 신경 써주어야 한다.
다음 코드는 백준 13159번 문제: 배열을 풀기 위해 구현한 splay tree이다. 문제에서 요구하지 않아 삽입/삭제 연산은 구현하지 않았지만, 원리를 이해한다면 직접 구현하기 어렵지 않을 것이다.
constexpr int N = 3e5;
struct Node {
Node *l, *r, *p;
int item, subtree, mn, mx;
long long sum;
bool reverse;
Node() {
l = r = p = nullptr;
item = subtree = mn = mx = 0;
sum = 0;
reverse = false;
}
} *tree, *nodes[N];
void propagate(Node* x) {
if (!x->reverse)
return;
swap(x->l, x->r);
x->reverse = false;
if (x->l)
x->l->reverse ^= 1;
if (x->r)
x->r->reverse ^= 1;
}
void update(Node* x) {
if (x->l)
propagate(x->l);
if (x->r)
propagate(x->r);
x->subtree = 1 + (x->l ? x->l->subtree : 0) + (x->r ? x->r->subtree : 0);
x->sum = x->item + (x->l ? x->l->sum : 0) + (x->r ? x->r->sum : 0);
x->mn = x->mx = x->item;
if (x->l) {
x->mn = min(x->mn, x->l->mn);
x->mx = max(x->mx, x->l->mx);
}
if (x->r) {
x->mn = min(x->mn, x->r->mn);
x->mx = max(x->mx, x->r->mx);
}
}
void rotate(Node* x) {
Node* p = x->p;
Node* b = nullptr;
propagate(p);
propagate(x);
if (p->l == x) {
p->l = b = x->r;
x->r = p;
} else {
p->r = b = x->l;
x->l = p;
}
x->p = p->p;
p->p = x;
if (b)
b->p = p;
if (x->p) {
if (x->p->l == p)
x->p->l = x;
else
x->p->r = x;
} else {
tree = x;
}
update(p);
update(x);
}
void splay(Node* x) {
propagate(x);
while (x->p) {
Node* p = x->p;
Node* g = x->p->p;
if (g) {
if ((g->l == p) == (p->l == x))
rotate(p);
else
rotate(x);
}
rotate(x);
}
}
Node* kth(int k) {
Node* curr = tree;
while (true) {
propagate(curr);
int x = curr->l ? curr->l->subtree : 0;
if (k == x) {
break;
} else if (k < x) {
curr = curr->l;
} else {
k -= x + 1;
curr = curr->r;
}
}
splay(curr);
return curr;
}
Node* getRange(int l, int r) {
Node* ret = nullptr;
int n = tree->subtree;
if (l > 0) {
kth(l - 1);
if (r < n - 1) {
Node* oldT = tree;
tree->r->p = nullptr;
tree = tree->r;
kth(r - l + 1);
ret = tree->l;
tree->p = oldT;
oldT->r = tree;
tree = oldT;
} else {
ret = tree->r;
}
} else {
if (r < n - 1) {
kth(r + 1);
ret = tree->l;
} else {
ret = tree;
}
}
return ret;
}
void reverse(int l, int r) {
Node* range = getRange(l, r);
range->reverse ^= 1;
}
출처
Previous post
Z 알고리즘Next post
Splay Tree 2. 시간복잡도의 증명