Z 알고리즘

길이가 $n$인 문자열 $s$의 Z 배열 $z[i]$는 $s[i]$에서 시작하는 부분 문자열이면서 $s$의 prefix이기도 한 가장 긴 문자열의 길이를 담는 배열이다. Z 배열을 통해서 패턴 매칭 문제 등을 해결할 수 있다.

Z 알고리즘을 사용해 Z 배열을 $O(n)$시간에 구하는 방법을 알아보자.

Z 배열 구하기

문자열이 ABCABCABAB일 때, Z 배열은 다음과 같다.

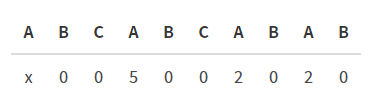
KMP나 Suffix array, LCP array와 마찬가지로 Z 알고리즘 역시 지금까지 구한 이전의 정보들을 최대한 활용해 시간 복잡도를 줄인다.

Z 알고리즘에서는 구간 $[l, \space r]$을 관리하며 Z 배열의 값을 $i = 1$부터 $n - 1$까지 하나씩 구한다. 이때 구간 $[l, \space r]$은 $s[l \dots r] = s[0 \dots r-l]$인 가장 큰 $r$과 그에 대응하는 $l$로 유지된다(처음엔 $[0, \space 0]$으로 초기화 한다). 이 구간을 이용해 다음 원소들의 값을 효율적으로 구할 수 있다. $z[0 \dots i - 1]$를 계산한 상태에서 $z[i]$를 구하는 상황에 가능한 경우를 모두 살펴보자.

(직접 예제 문자열을 가지고 그려보면 따라오기 쉽다.)

• case 1. $r < i$인 경우: 위치 $i$에 대해 아는 것이 없기 때문에 위치 $0$과 $i$에서 시작해 한 글자씩 비교해 $z[i]$를 구한다. 한 글자 이상 일치한다면 $[l, \space r]$이 $[i, \space i + z[i] - 1]$로 업데이트될 것이다.

• case 2. $r \ge i$인 경우: $s[l \dots r] = s[0 \dots r-l]$이고 $i$가 $[l, \space r]$구간에 존재한다. 따라서 $s[i \dots r]= s[i-l \dots r-l]$임을 알 수 있고, $z[i]$를 구하는데 $z[i-l]$의 정보를 활용할 수 있다.

  • 2.1. $i + z[i-l] - 1 < r$인 경우: 이미 알고있는 정보 $s[i \dots r] = s[i-l \dots r-l]$을 통해, $s[i]$에서 부터 시작하는 부분 문자열이면서 $s$의 prefix이기도 한 가장 긴 문자열이 위치 $r$ 전에 끝난다는 것을 알 수 있다. 따라서 $z[i] = z[i-l]$이다.

  • 2.2. $i + z[i-l] - 1 \ge r$인 경우: $z[i]$가 적어도 $r - i + 1$이상임을 알고 있지만, 위치 $r$이후에 대한 정보가 없으므로 위치 $r - i + 1$과 $r + 1$부터 시작해 한 글자씩 비교해 나간다. 한 글자 이상 일치한다면 $[l, \space r]$이 업데이트될 것이다.

작동방식을 생각하면 시간 복잡도는 $O(n)$이다. 위치 $r$ 이후의 문자만 비교하는 데 사용하고, 두 문자가 일치하면 $r$이 $1$ 이상 증가하기 때문에 $O(n)$번의 일치하는 비교가 있을 수 있다. 또 불일치하는 비교가 있을 때마다 비교가 종료되고 다음 $z$값을 구하므로 불일치하는 비교 역시 $O(n)$번 있을 수 있다.

구현 코드

작동방식을 그대로 옮겨 구현할 수 있다.

int x = 0;
int y = 0;

for (int i = 1; i < s.size(); i++) {
    if (i > y) {
        int j = 0;
        while (i + j < s.size() && s[j] == s[i + j]) {
            z[i]++;
            j++;
        }
    } else if (i + z[i - x] <= y) {
        z[i] = z[i - x];
    } else /* if (i + z[i - x] > y) */ {
        z[i] = y - i + 1;
        int j = y + 1;
        while (j < s.size() && s[j] == s[j - i]) {
            z[i]++;
            j++;
        }
    }

    if (i + z[i] - 1 > y) {
        y = i + z[i] - 1;
        x = i;
    }
}

더욱 짧고 최적화된 구현이다. (출처 - 코드포스 블로그 포스트)

int L = 0, R = 0;
for (int i = 1; i < n; i++) {
  if (i > R) {
    L = R = i;
    while (R < n && s[R-L] == s[R]) R++;
    z[i] = R-L; R--;
  } else {
    int k = i-L;
    if (z[k] < R-i+1) z[i] = z[k];
    else {
      L = i;
      while (R < n && s[R-L] == s[R]) R++;
      z[i] = R-L; R--;
    }
  }
}

i > R일 때 L = R = i를 했는데 s[0] != s[i]인 경우(한 글자도 일치하지 않는 경우) [L, R]이 구간의 정의와 일치하지 않게 된다. 그러나 이 경우 다음 z[i + 1]를 구하는 단계에서 i + 1 > R인 것은 변함이 없기 때문에 작동원리를 완벽하게 따르지 않아도 문제없이 작동하게 된다.

사용

Z 알고리즘을 통해 풀 수 있는 문제는 KMP나 Suffix array, LCP array로도 풀 수 있는 경우가 많다. 특히 KMP의 failure function은 Z 배열과 매우 유사하다. 그러나 Z 알고리즘은 작동방식이 직관적이고 코드가 비교적 간단하다.

문자열 $s$에서 패턴 $p$를 찾는 패턴 매칭 문제를 풀어보자. $p$와 $s$ 사이에 두 문자열에서 모두 등장하지 않는 문자 #을 끼워 넣은 새로운 문자열 $p$#$s$를 만들고, 이 문자열의 Z array를 구하자. Z array를 순회하면서 원소의 값이 $p$의 길이와 같은 index를 찾으면 된다.

또한 어떤 문자열의 prefix이면서 동시에 suffix인 부분 문자열을 border라고 하는데, 이 border와 관련된 문제를 다른 알고리즘보다 쉽게 풀 수 있다. 예를 들어 모든 border를 쉽게 구할 수 있는데, $s[i ... n-1]$가 $s$의 border인 것은 $i + z[i] = n$인 것과 동치이기 때문이다.

출처: 코드포스 블로그 포스트, 알고리즘 트레이닝: 프로그래밍 대회 입문 가이드